Rasmiy til
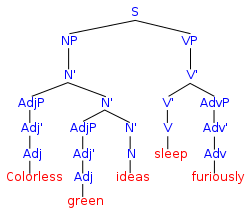
Mantiq, matematika, informatika va tilshunoslikda rasmiy til harflari alifbodan olingan va maʼlum qoidalar toʻplamiga muvofiq yaxshi shakllangan soʻzlardan iborat.
Rasmiy tilning alifbosi til qatorlariga birikadigan harflar yoki belgilardan iborat[1]. Ushbu alifbo belgilaridan birlashtirilgan har bir qator soʻz deb ataladi va maʼlum bir rasmiy tilga tegishli soʻzlar baʼzan yaxshi shakllangan soʻzlar yoki yaxshi shakllangan formulalar deb ataladi. Rasmiy til koʻpincha uni shakllantirish qoidalaridan tashkil topgan oddiy grammatika yoki kontekstsiz grammatika kabi rasmiy grammatika orqali aniqlanadi.
Informatika sohasida rasmiy tillar dasturlash tillarining grammatikasini va tabiiy tillar kichik toʻplamlarining rasmiylashtirilgan versiyalarini aniqlash uchun asos sifatida ishlatiladi.Bunda til soʻzlari maʼlum maʼnolar yoki semantika bilan bogʻliq boʻlgan tushunchalarni ifodalaydi.
Rasmiy til nazariyasi sohasi, birinchi navbatda, bunday tillarning sof sintaktik tomonlarini, yaʼni ularning ichki strukturaviy qonuniyatlarini o‘rganadi. Rasmiy til nazariyasi tabiiy tillarning sintaktik qonuniyatlarini tushunish usuli sifatida tilshunoslikdan paydo boʻldi.
Tarixi
[tahrir | manbasini tahrirlash]XVII asrda Gotfrid Leybnits piktogrammalardan foydalanadigan universal va rasmiy til boʻlgan universal tilni tasvirlab berdi. Bu davrda Gauss Gauss kodlari muammosini ham tadqiq qildi[2].
Gottlob Frege attempted to realize Leibniz’s ideas, through a notational system first outlined in Begriffsschrift (1879) and more fully developed in his 2-volume Grundgesetze der Arithmetik (1893/1903).[3] This described a „formal language of pure language.“[4]
XX asrning birinchi yarmida rasmiy tillar bilan bogʻliq bir qancha ishlanmalar amalga oshirildi. Axel Thue 1906-yildan 1914-yilgacha soʻzlar va tilga oid toʻrtta maqola chop etdi. Emil Post keyinchalik „Thue Systems“ deb atagan narsani taqdim etdi[5]. Keyinchalik Post ushbu maqoladan rasmiy tillarni yaratish uchun kanonik tizimni ishlab chiqdi.
Noam Xomskiy Xomskiy iyerarxiyasi deb nomlanuvchi rasmiy va tabiiy tillarning mavhum tasvirini ishlab chiqdi[6]. 1959-yilda Jon Backus FORTRANni yaratganidan soʻng yuqori darajadagi dasturlash tilining sintaksisini tavsiflash uchun Backus-Naur shaklini ishlab chiqdi[7]. Piter Naur 1960-yilda xuddi shunday sxemani ixtiro qilgan.
Alifbodagi soʻzlar
[tahrir | manbasini tahrirlash]Rasmiy tillar kontekstida alifbo har qanday toʻplam boʻlishi mumkin, garchi koʻpincha soʻzning odatiy maʼnosida alifboni yoki umuman olganda, ASCII yoki Unicode kabi har qanday chekli belgilarni kodlashdan foydalanish mantiqiy boʻladi. Alfavit elementlariga uning harflari deyiladi. Alifbo cheksiz koʻp elementlardan iborat boʻlishi mumkin.Ammo rasmiy til nazariyasidagi koʻpgina taʼriflar cheklangan miqdordagi elementlarga ega alifbolarni belgilaydi va koʻpchilik natijalar faqat ularga tegishli boʻladi.
Alifbodagi soʻz har qanday chekli harflar ketma-ketligi (yaʼni, qator) boʻlishi mumkin. S alifbosidagi barcha soʻzlar toʻplami odatda S * bilan belgilanadi (Kleene yulduzi yordamida). Soʻzning uzunligi u tuzilgan harflar soni bilan tavsiflanadi. Har qanday alifbo uchun uzunligi 0 boʻlgan faqat bitta soʻz mavjudva u boʻsh soʻz deb ataladi. Boʻsh soʻz koʻpincha, e, e, l yoki hatto l bilan belgilanadi. Ikki so‘zni birlashtirib, yangi so‘z hosil qilish mumkin, uning uzunligi asl so‘zlarning uzunliklari yig‘indisiga teng. So‘zning bo‘sh so‘z bilan bog‘lanishi natijasida asli so‘z hosil bo‘ladi.
Baʼzi ilovalarda, ayniqsa mantiqda, alifbo lugʻat va formulalar yoki jumlalar sifatida ham tanilgan. .
Taʼrifi
[tahrir | manbasini tahrirlash]S alifbosidagi rasmiy til L — bu S * ning kichik toʻplami, yaʼni shu alifbo ustidagi soʻzlar toʻplami. Baʼzan soʻzlar toʻplami iboralarga guruhlanadi. „Yaxshi shakllangan iboralar“ yaratish uchun qoidalar va cheklovlar ishlab chiqilishi mumkin.
„Rasmiy til“ tushunchasining haqiqiy taʼrifi: berilgan alifbodan tuzilgan chekli uzunlikdagi satrlarning (ehtimol cheksiz) toʻplami.
Misollar
[tahrir | manbasini tahrirlash]L alifbosida S={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:
- Tarkibida „+“ yoki „=" boʻlmagan va "0“ bilan boshlanmagan har bir boʻsh qator mavjud L .

Ushbu diagrammada rasmiy tizim ichidagi sintaktik boʻlinishlar koʻrsatilgan. Belgilar qatorlarini yaxshi shakllangan formulalarga boʻlish mumkin. Yaxshi shakllangan formulalar toʻplami teorema va teorema boʻlmaganlarga boʻlinadi. - „0“ qatori mavjud L .
- „=" dan iborat qator mavjud L faqat bitta "=“ boʻlsa va u ikkita haqiqiy satrni ajratsa L .
- Tarkibida „+“ boʻlgan, lekin „=“ boʻlmagan qator mavjud L, agar satrdagi har bir „+“ ikkita haqiqiy qatorni ajratsa L .
Ushbu qoidalarga koʻra, „23+4=555“ qatori mavjud L, lekin „=234=+“ qatori emas. Bu rasmiy til natural sonlar, yaxshi shakllangan qoʻshimchalar va yaxshi shakllangan qoʻshilish tengliklarini ifodalaydi, lekin ular nimani anglatishini (semantikasi) emas, balki faqat qanday koʻrinishini (ularning sintaksisi) ifodalaydi. Masalan, ushbu qoidalarning hech bir joyida „0“ nol sonini, „+“ qo‘shishni, „23+4=555“ noto‘g‘ri ekanligini va hokazo degan ko‘rsatma yo‘q.
Qurilishlar
[tahrir | manbasini tahrirlash]Cheklangan tillar uchun barcha yaxshi tuzilgan soʻzlarni aniq sanab oʻtish mumkin. Masalan, biz tilni tasvirlashimiz mumkin L, xuddi L = {a, b, ab, cba}. Ushbu konstruktsiyaning degenerativ holati boʻsh til boʻlib, unda umuman soʻz yoʻq (L = ∅).
Biroq, hatto S kabi cheklangan (boʻsh boʻlmagan) alifboda ham = {a, b} potentsial sifatida ifodalanishi mumkin boʻlgan cheksiz sonli soʻzlar mavjud: „a“, „abb“, „ababba“, „aaababbbbaab“, . . . . Shuning uchun rasmiy tillar odatda cheksizdir va cheksiz rasmiy tilni tavsiflash L yozish kabi oddiy emas.L = {a, b, ab, cba}.
Tilning spetsifikatsiyasi rasmiyatchiliklari
[tahrir | manbasini tahrirlash]Rasmiy tillar bir nechta fanlarda vosita sifatida ishlatiladi. Biroq, rasmiy til nazariyasi kamdan-kam hollarda alohida tillar bilan bogʻliq, lekin asosan tillarni tavsiflash uchun turli xil rasmiyatchiliklarni oʻrganish bilan bogʻliq. Masalan, til sifatida berilishi mumkin
- baʼzi bir rasmiy grammatika tomonidan yaratilgan satrlar;
- maʼlum bir muntazam ifoda bilan tasvirlangan yoki mos keladigan satrlar;
- Tyuring mashinasi yoki chekli holat avtomati kabi baʼzi avtomatlar tomonidan qabul qilingan satrlar;
- baʼzi qaror qabul qilish protseduralari (bogʻliq HA/YOʻQ savollari ketma-ketligini soʻraydigan algoritm) HA javobini beradigan qatorlar.
Bunday rasmiyatchiliklar haqida soʻraladigan odatiy savollarga quyidagilar kiradi:
- Ularning ifoda kuchi nimada? (X formalizm Y tasvirlashi mumkin boʻlgan har bir tilni tasvirlay oladimi? U boshqa tillarni tasvirlay oladimi?)
- Ularning tan olinishi nimada? (Maʼlum bir soʻz X formalizm bilan tavsiflangan tilga tegishli yoki yoʻqligini aniqlash qanchalik qiyin?)
- Ularning solishtirish qobiliyati qanday? (Biri X formalizmda, ikkinchisi Y formatida yoki yana Xda tasvirlangan ikkita til aslida bir xil til ekanligini aniqlash qanchalik qiyin?).
Ajablanarlisi shundaki, koʻpincha bu qaror muammolariga javob „buni umuman qilish mumkin emas“ yoki „bu juda qimmat“. Shuning uchun, rasmiy til nazariyasi hisoblash nazariyasi va murakkablik nazariyasining asosiy qoʻllanishi sohasidir. Rasmiy tillar Xomskiy iyerarxiyasida generativ grammatikasining ifoda kuchiga, shuningdek, tanib olish avtomatining murakkabligiga qarab tasniflanishi mumkin. Kontekstsiz grammatika va oddiy grammatika ekspressivlik va tahlil qilish qulayligi oʻrtasida yaxshi kelishuvni taʼminlaydi va amaliy dasturlarda keng qoʻllanadi.
Manbalar
[tahrir | manbasini tahrirlash]- ↑ See e.g. Reghizzi, Stefano Crespi. Formal Languages and Compilation, Texts in Computer Science. Springer, 2009 — 8-bet. ISBN 9781848820500. „An alphabet is a finite set“
- ↑ „In the prehistory of formal language theory: Gauss Languages“ (1992-yil yanvar). Qaraldi: 2021-yil 30-aprel.
- ↑ „Gottlob Frege“ (2019-yil 5-dekabr). Qaraldi: 2021-yil 30-aprel.
- ↑ Martin Davis „Influences of Mathematical Logic on Computer Science“, . The universal Turing machine: a half-century survey Rolf Herken: . Springer, 1995 — 290-bet. ISBN 978-3-211-82637-9.
- ↑ „Thue’s 1914 paper: a translation“ (2013-yil 28-avgust). Qaraldi: 2021-yil 30-aprel.
- ↑ Jager, Gerhard; Rogers, James (19 July 2012). "Formal language theory: refining the Chomsky hierarchy". Philosophical Transactions of the Royal Society B 367 (1598). doi:10.1098/rstb.2012.0077.
- ↑ „John Warner Backus“ (2016-yil fevral). Qaraldi: 2021-yil 30-aprel.

