Tomografik rekonstruksiya

Tomographic reconstruction: Projection, Back projection and Filtered back projection

Tomografik rekonstruksiya koʻp oʻlchovli teskari muammoning bir turi boʻlib, u yerda qiyinchilik cheklangan miqdordagi proektsiyalardan maʼlum bir tizimning taxminini berishdir. Tomografik tasvirlashning matematik asoslari Iogann Radon tomonidan yaratilgan. Ilovalarning diqqatga sazovor namunasi kompyuter tomografiyasini (KT) rekonstruksiya qilish boʻlib, unda bemorlarning kesma tasvirlari invaziv boʻlmagan usulda olinadi. Soʻnggi ishlanmalar, aeroport xavfsizligida kompyuter tomografiyasidan foydalanishni sinash va baholash uchun zarur boʻlgan real ob’ektni kiritish bilan bogʻliq vazifalar uchun Radon transformatsiyasi va uning teskarisini koʻrdi.

Ushbu maqola umuman tomografiyaning barcha turlarini qayta tiklash usullariga taalluqlidir, ammo baʼzi atamalar va fizik tavsiflar toʻgʻridan-toʻgʻri rentgen kompyuter tomografiyasini qayta tiklashga ishora qiladi.

Formula bilan tanishtirish.

1-rasm: Tomografiya va tomografik rekonstruksiyada qoʻllanadigan parallel nurli geometriya. Muayyan burchak ostida tomografiya natijasida hosil boʻlgan har bir proyeksiya ob’ekt orqali chiziqli integrallar toʻplamidan iborat.

Bosh suyagining plastik fantomidan olingan tomografik tasvir. Proyeksiyalangan rentgen nurlari kompyuter tomografiyasi bilan olingan bu boʻlakda tasvir artefaktlari sifatida aniq koʻrinadi, chunki burchaklar ustidagi proyeksiya boʻlaklarining cheklangan miqdori.

Berilgan burchak ostida tomografik oʻlchash jarayoni natijasida yuzaga keladigan ob’ektning proyeksiyasi $\theta$, chiziqli integrallar toʻplamidan tashkil topgan (1-rasmga qarang). 2Dda tashkil etilgan turli burchak ostidagi koʻplab bunday proyeksiyalar toʻplami sinogramma deb ataladi (3-rasmga qarang). X-nurli KTda chiziqli integrali rentgen nurlari nurlarining ob’ekt boʻylab toʻgʻri chiziq boʻylab harakatlanishining umumiy zaiflashuvini ifodalaydi. Yuqorida aytib oʻtilganidek, natijada olingan tasvir zaiflashuv koeffitsientining 2D (yoki 3D) modelidir. Yaʼni, biz tasvirni topishni xohlaymiz $\mu (x,y)$ . Skanerlash usulini tasavvur qilishning eng oddiy va eng oson usuli – bu tizimdir parallel proyeksiya, birinchi skanerlarda qoʻllangan. Ushbu munozara uchun biz toʻplanishi kerak boʻlgan maʼlumotlarni pozitsiyada parallel nurlar qatori sifatida koʻrib chiqamiz $r$, burchak ostidagi proyeksiya boʻylab $\theta$ . Bu turli burchaklar uchun takrorlanadi. Attenuatsiya toʻqimalarda eksponent ravishda sodir boʻladi:

$I=I_{0}\exp \left({-\int \mu (x,y)\,ds}\right)$

qayerda $\mu (x,y)$ pozitsiyaga bogʻliq boʻlgan zaiflashuv koeffitsienti. Shuning uchun, odatda, umumiy zaiflashuv $p$ holatidagi nurning $r$, burchakdagi proyeksiyada $\theta$, chiziqli integrali bilan berilgan:

$p_{\theta }(r)=\ln \left({\frac {I}{I_{0}}}\right)=-\int \mu (x,y)\,ds$

1-rasmdagi koordinatalar sistemasidan foydalanib, ning qiymati $r$ qaysi nuqtada $(x,y)$ burchak ostida proyeksiya qilinadi $\theta$ tomonidan beriladi:

$x\cos \theta +y\sin \theta =r\$

Shunday qilib, yuqoridagi tenglamani quyidagicha qayta yozish mumkin

$p_{\theta }(r)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\delta (x\cos \theta +y\sin \theta -r)\,dx\,dy$

qayerda $f(x,y)$ ifodalaydi $\mu (x,y)$ va $\delta ()$ Dirac delta funktsiyasidir . Ushbu funktsiya 2D ob’ektining Radon transformatsiyasi (yoki sinogrammasi) sifatida tanilgan.

Proyeksiyaning Furye transformatsiyasini quyidagicha yozish mumkin

$P_{\theta }(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\exp[-j\omega (x\cos \theta +y\sin \theta )]\,dx\,dy=F(\Omega _{1},\Omega _{2})$ qayerda $\Omega _{1}=\omega \cos \theta ,\Omega _{2}=\omega \sin \theta$

$P_{\theta }(\omega )$ ning 2D Furye konvertatsiyasining bir qismini ifodalaydi $f(x,y)$ burchak ostida $\theta$ . Teskari Furye transformatsiyasidan foydalanib, teskari Radon transformatsiyasi formulasini osongina olish mumkin.

$f(x,y)={\frac {1}{2\pi }}\int \limits _{0}^{\pi }g_{\theta }(x\cos \theta +y\sin \theta )d\theta$

qayerda $g_{\theta }(x\cos \theta +y\sin \theta )$ ning Hilbert konvertatsiyasining hosilasidir $p_{\theta }(r)$

Nazariy jihatdan, radonning teskari oʻzgarishi asl tasvirni beradi. Proyeksiya-kesim teoremasi shuni aytadiki, agar bizda cheksiz koʻp burchak ostida olingan ob’ektning cheksiz sonli bir oʻlchovli proyeksiyalari boʻlsa, biz asl ob’ektni mukammal tarzda qayta qurishimiz mumkin, $f(x,y)$ . Biroq, amalda faqat cheklangan miqdordagi proyeksiyalar mavjud boʻladi.

Taxmin qilib $f(x,y)$ samarali diametrga ega $d$ va kerakli rezolyutsiya $R_{s}$, rekonstruksiya qilish uchun zarur boʻlgan proektsiyalarning umumiy qoidasi $N>\pi d/R_{s}$

Qayta qurish algoritmlari

Uch oʻlchamli ob’ektni uning proyeksiyalaridan rekonstruksiya qilish jarayonini amalga oshirish uchun amaliy qayta qurish algoritmlari ishlab chiqilgan. Ushbu algoritmlar asosan Radon transformatsiyasining matematikasiga, maʼlumotlarni yigʻish jarayonining statistik bilimlariga va maʼlumotlarni tasvirlash tizimining geometriyasiga asoslangan.

Furye-domenni qayta qurish algoritmi

Qayta qurish interpolyatsiya yordamida amalga oshirilishi mumkin. Faraz qilaylik $N$ prognozlari $f(x,y)$ teng oraliq burchaklarda hosil boʻladi, har biri bir xil tezlikda namuna olinadi. Har bir proyeksiyada diskret Furye konvertatsiyasi (DFT) chastota domenida namuna olish imkonini beradi. Chastotadan olingan barcha proyeksiyalarni birlashtirib, chastota domenida qutbli rastr hosil boʻladi. Polar rastr siyrak, shuning uchun nomaʼlum DFT nuqtalarini toʻldirish uchun interpolyatsiya qoʻllanadi va rekonstruksiya teskari diskret Furye konvertatsiyasi orqali amalga oshirilishi mumkin. Qayta qurish samaradorligi qutbli rastrning siyrakligini oʻzgartirish usullarini loyihalash orqali yaxshilanishi mumkin, bu interpolyatsiya samaradorligini oshiradi.

Masalan, chastota domenidagi konsentrik kvadrat rastrni har bir proyeksiya orasidagi burchakni quyidagi tarzda oʻzgartirish orqali olish mumkin:

$\theta '={\frac {R_{0}}{\max\{|\cos \theta |,|\sin \theta |\}}}$

qayerda $R_{0}$ baholash uchun eng yuqori chastota hisoblanadi.

Konsentrik kvadrat rastr barcha interpolyatsiya pozitsiyalarini toʻrtburchaklar DFT panjarasida boʻlishiga imkon berib, hisoblash samaradorligini oshiradi. Bundan tashqari, u interpolyatsiya xatosini kamaytiradi. Shunga qaramay, Furye-Transform algoritmi oʻz-oʻzidan shovqinli chiqishni ishlab chiqarishning kamchiliklariga ega.

Orqaga proyeksiya qilish algoritmi

Tomografik tasvirni qayta tiklash amaliyotida koʻpincha filtrlangan orqaga proyeksiya algoritmi deb nomlanuvchi teskari Radon transformatsiyasining barqarorlashtirilgan va diskretlashtirilgan versiyasi qoʻllanadi.

Namuna olingan diskret tizim bilan teskari Radon transformatsiyasi hisoblanadi

$f(x,y)={\frac {1}{2\pi }}\sum _{i=0}^{N-1}\Delta \theta _{i}g_{\theta _{i}}(x\cos \theta _{i}+y\sin \theta _{i})$

$g_{\theta }(t)=p_{\theta }(t)\cdot k(t)$

qayerda $\Delta \theta$ proyeksiyalar orasidagi burchak oraligʻi va $k(t)$ chastotali javobga ega Radon yadrosidir $|\omega |$ .

Orqa proyeksiya nomi ikki oʻlchovli signalni olish uchun bir oʻlchovli proyeksiyani bir oʻlchovli Radon yadrosi (orqaga proyeksiyalangan) tomonidan filtrlash kerakligidan kelib chiqadi. Amaldagi filtrda toʻgʻridan-toʻgʻri toʻgʻridan-toʻgʻri kuchlanishni oʻz ichiga olmaydi, shuning uchun doimiy toʻgʻridan-toʻgʻri chiziqni qoʻshish maqsadga muvofiqdir. Orqa proyeksiya yordamida rekonstruksiya yuqorida tavsiflangan interpolyatsiya usuliga qaraganda yaxshiroq rezolyutsiyaga imkon beradi. Biroq, u koʻproq shovqinni keltirib chiqaradi, chunki filtr yuqori chastotali tarkibni kuchaytirishga moyil.

Takroriy qayta qurish algoritmi

Iterativ algoritm hisoblashni talab qiladi, lekin u tizim haqida apriori maʼlumotlarni kiritish imkonini beradi. $f(x,y)$ .

Mayli $N$ proyeksiyalar soni va $D_{i}$ uchun buzilish operatori boʻling $i$ burchak ostida olingan th proyeksiyasi $\theta _{i}$ . $\{\lambda _{i}\}$ iteratsiyalarni konvertatsiya qilishni optimallashtirish uchun parametrlar toʻplamidir.

$f_{0}(x,y)=\sum _{i=1}^{N}\lambda _{i}p_{\theta _{i}}(r)$

Turli sensor oraligʻi bilan Shepp-Logan Phantomning fan-nurli rekonstruktsiyasi. Datchiklar orasidagi kichikroq masofa yanada nozik qayta qurish imkonini beradi. Rasm MATLAB yordamida yaratilgan.

$f_{k}(x,y)=f_{k-1}(x,y)+\sum _{i=1}^{N}\lambda _{i}[p_{\theta _{i}}(r)-D_{i}f_{k-1}(x,y)]$

Rekursiv tomografik rekonstruksiya algoritmlarining muqobil oilasi algebraik rekonstruksiya usullari va iterativ siyrak asimptotik minimal variatsiyadir .

Fan-nurni qayta qurish

Kollimatsiyalanmagan fan nuridan foydalanish keng tarqalgan, chunki kollimatsiyalangan nurlanish nurini olish qiyin. Fan nurlari proyeksiyalar sifatida bir-biriga parallel emas, qator chiziqli integrallarni hosil qiladi. Fan-nur tizimi 360 graduslik burchak oraligʻini talab qiladi, bu mexanik cheklovlarni keltirib chiqaradi, ammo bu signalni tezroq olish vaqtini beradi, bu tibbiyot sohasida kabi baʼzi sharoitlarda foydali boʻlishi mumkin. Orqaga proyeksiya ikki bosqichli shunga oʻxshash protsedura boʻlib, filtrlangan proyeksiyalardan olingan ogʻirlikli yigʻindili orqa proyeksiyalarni hisoblash yoʻli bilan qayta qurish imkonini beradi.

Chuqur taʼlimni qayta qurish

Puasson shovqini U-Net mavjud yuqori kontrastli lezyonga oʻxshash ob’ektni qayta qurishda muvaffaqiyatsizlikka olib keladigan chuqur oʻrganishni qayta qurishda Puasson shovqinining taʼsiri.

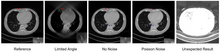
Chuqur oʻrganish usullari bugungi kunda tasvirni qayta tiklashda keng qoʻllanadi va tasvirni qayta tiklashning turli vazifalarida, jumladan, past dozali denozizatsiya, siyrak koʻrinishdagi rekonstruksiya, cheklangan burchakli tomografiya va metall artefaktni kamaytirishda ajoyib natijalarga erishdi. Ajoyib sharhni IEEE Transaction on Medical Imaging maxsus sonida topish mumkin . Chuqur oʻrganishni qayta qurish algoritmlarining bir guruhi tasvirni tasvirga qayta tiklashga erishish uchun post-processing neyron tarmoqlarini qoʻllaydi, bu yerda kirish tasvirlari anʼanaviy rekonstruksiya usullari bilan qayta tiklanadi. Cheklangan burchakli tomografiyada U-Net yordamida artefaktni kamaytirish bunga misol boʻla oladi. Biroq, rasmda koʻrsatilganidek, toʻliq maʼlumotlarga asoslangan usul bilan qayta tiklangan tasvirda notoʻgʻri tuzilmalar paydo boʻlishi mumkin . Shuning uchun, aniq oʻrganish kontseptsiyasida tasvirlanganidek, maʼlum operatorlarni neyron tarmoqlarning arxitektura dizayniga integratsiyalashuvi foydali koʻrinadi. Masalan, proyeksiya maʼlumotlaridan toʻgʻridan-toʻgʻri tasvirni qayta tiklashni filtrlangan orqa proyeksiya doirasidan oʻrganish mumkin. Yana bir misol, takroriy rekonstruksiya algoritmlarini ochish orqali neyron tarmoqlarni qurishdir. Aniq oʻrganishdan tashqari, chuqur oʻrganishni qayta qurish bilan anʼanaviy qayta qurish usullaridan foydalanish ham chuqur oʻrganishni qayta qurish tasvir sifatini yaxshilash uchun muqobil yondashuv hisoblanadi.

Tomografik rekonstruksiya dasturi

Moslashuvchan tomografik rekonstruksiya uchun PYRO-NN, TomoPy, CONRAD, ODL, ASTRA asboblar qutisi, va TIGRE kabi ochiq manbali asboblar qutilari mavjud. TomoPy – bu Argonna milliy laboratoriyasidagi ilgʻor foton manbasida tomografik maʼlumotlarni qayta ishlash va tasvirni qayta tiklash vazifalarini bajarish uchun ochiq manba Python asboblar toʻplami. TomoPy asboblar toʻplami sinxrotron moslamasining nur chizigʻida foydalanish va joylashtirish uchun qulay boʻlishi uchun maxsus ishlab chiqilgan. U Scientific Data Exchange (Scientific Data Exchange) orqali diskdan koʻplab umumiy sinxrotron maʼlumotlar formatlarini oʻqishni qoʻllab-quvvatlaydi va sinxrotron maʼlumotlari uchun keng tarqalgan ishlatiladigan bir qancha boshqa ishlov berish algoritmlarini oʻz ichiga oladi. TomoPy shuningdek, bir nechta rekonstruksiya algoritmlarini oʻz ichiga oladi, ular koʻp yadroli ish stantsiyalarida va keng koʻlamli hisoblash qurilmalarida ishlaydi. ASTRA Toolbox bu MATLAB va Python 2D va 3D tomografiya uchun yuqori unumli GPU primitivlari asboblar toʻplami boʻlib, 2009 yildan 2014 yilgacha Antverpen universiteti iMinds-Vision Lab tomonidan ishlab chiqilgan va 2014 yildan beri iMinds-VisionLabsion (VisionLab-Vi) tomonidan birgalikda ishlab chiqilgan., UAntverpen va CWI, Amsterdam. Asboblar qutisi yuqori moslashuvchan manba/detektor joylashuvi bilan parallel, fan va konus nurlarini qoʻllab-quvvatlaydi. TomoPy va ASTRA asboblar toʻplami, jumladan FBP, Gridrec, ART, SIRT, SART, BART, CGLS, PML, MLEM va OSEM orqali koʻplab qayta qurish algoritmlari mavjud. 2016 yilda ASTRA asboblar toʻplami TomoPy tizimiga birlashtirildi. ASTRA asboblar toʻplamini TomoPy tizimiga integratsiyalashgan holda, optimallashtirilgan GPU asosidagi rekonstruksiya usullari sinxrotron nur chizigʻi foydalanuvchilari uchun osonlik bilan mavjud boʻladi va ASTRA asboblar toʻplami foydalanuvchilari maʼlumotlarni osonroq oʻqishlari va maʼlumotlarni filtrlash va artefaktni tuzatish uchun TomoPy’ning boshqa funksiyalaridan foydalanishlari mumkin.

Miyaning tomografiyasi nimani koʻrsatishi mumkin? Shikast miya shikastlanishi uchun kompyuter tomografiyasi. Miyaning anʼanaviy kompyuter tomografiyasi

Miyaning KTsi diagnostikada juda keng tarqalgan tekshiruv boʻlib, yumshoq toʻqimalarning tuzilishini oʻrganish, oʻsmalar va anormalliklarni aniqlash, shikastlanishdan keyin yalligʻlanish jarayonlari, buzilishlar va shikastlanishlarni aniqlash uchun buyuriladi. Boshning KT-si juda koʻp koʻrsatkichlarga ega, chunki diagnostika boʻyicha ushbu tekshiruv turi yuqori aniqlik va axborot tarkibi bilan ajralib turadi. KT uchun kontrendikatsiyalar boʻlsa, MRI yoki ultratovush muqobil boʻladi.

Boshning tomografiyasi nimani koʻrsatadi? KT tomografiyasi quyidagi koʻrsatkichlar uchun koʻrsatiladi:

miya shikastlanishining chayqalishi, shishishi, qon ketishi va boshqa oqibatlari;

qon aylanishining buzilishiga (qon tomiriga) shubha;

xoʻppozlar, kistalar (siz kistalarning tabiatini oʻrnatishingiz mumkin);

yalligʻlanish jarayonlari;

yuqumli jarayonlar (meningit, ensefalit, ensefalopatiya);

yaxshi xulqli oʻsmalarni aniqlash uchun va malign neoplazmalar, metastazlar (KT ham, SCT ham buyurilishi mumkin);

miyaning tuzilmalari va qon tomir tizimining rivojlanishidagi anormallik;

anevrizma, tromboz;

gidrosefali (toʻqimalarda miya omurilik suyuqligining ortiqcha toʻplanishi);

konvulsiyalar, loyqa koʻrish, chalkashlik, bosh aylanishi, sezgirlikning pasayishi;

operatsiyalardan oldin tadqiqotlar, operatsiyadan keyingi nazorat;

ikki yoki uch oy davomida tushunarsiz tabiatning doimiy bosh ogʻrigʻining sabablarini aniqlash;

mRG oʻtkazilmasligi (yurak stimulyatori, insulin pompasi, tanadagi metall buyumlar mavjudligi).

Gipofiz bezi tomografiyasi

Gipofizning tomografik tekshiruvi suyaklar va boʻshliqlarni tekshirish uchun yuboriladi. U uzluksiz yumshoq toʻqimalardan tashkil topganligi sababli, uni tekshirish uchun MRI tekshiruviga yuboriladi. MRI uchun kontrendikatsiya holatlarida buyuriladi. Ammo bu holatda natijalar har doim ham toʻliq boʻlmasligi mumkin.