Kristallografik nuqsonlar

Kristallografik nuqsonlar kristalli qattiq jismlardagi muntazam panjara shaklining buzilishidir. Ular tez-tez uchraydi, chunki davriy kristall tuzilishga ega boʻlgan kristallardagi takrorlanuvchi yacheyka takroriy joylashuvchi atomlar yoki molekulalarning joylashuvi mukammal boʻlmaydi[2][3][4].
Nuqtaviy nuqsonlar
[tahrir | manbasini tahrirlash]Nuqtaviy nuqsonlar faqat bitta panjara nuqtasida yoki uning atrofida yuzaga keladigan nuqsonlardir. Ular fazoda hech qanday oʻlchamda kengaytirilmaydi. Nuqtaviy nuqsonning qanchalik kichikligi oʻlcham bilan chegaralanganligi odatda aniq belgilanmaydi. Biroq, bu nuqsonlar odatda koʻpi bilan bir nechta qoʻshimcha yoki yetishmayotgan atomlarni oʻz ichiga oladi. Mavjud kristall strukturadagi katta nuqsonlar odatda dislokatsiya halqalari hisoblanadi. Tarixiy sabablarga koʻra, koʻplab nuqtaviy nuqsonlar, ayniqsa ion kristallari, markazlar deb ataladi: masalan, koʻplab ionli qattiq jismlardagi boʻsh joy luminesans markazi, rang markazi yoki F-markazi deb ataladi. Ushbu dislokatsiyalar elektrokimyoviy reaksiyalarga olib keladigan kristallar orqali ionlarni tashish imkonini beradi. Ular koʻpincha Kröger-Vink belgisi yordamida belgilanadi.
- Boʻsh joy nuqsonlari (vakansiya) — bu mukammal kristaldagi boʻsh boʻlgan panjara joylari (tugunlar). Agar qoʻshni atom boʻsh joyni egallash uchun harakat qilsa, boʻsh joy shu atom egallagan joyga qarama-qarshi yoʻnalishda harakat qiladi. Atrofdagi kristall strukturaning barqarorligi qoʻshni atomlarning boʻsh joyga kelib oʻtirmasaligini taʼminlaydi. Baʼzi materiallarda qoʻshni atomlar boʻsh joydan uzoqlashadilar, chunki ularga atrofdagi atomlarning tortishish kuchi taʼsir etadi. Vakansiya (yoki ionli qattiq jismdagi boʻsh joylar juftligi) baʼzan Shottki nuqsoni deb ataladi.
- Interstitsial nuqsonlar kristall strukturasida odatda atom boʻlmagan joyni egallagan atomlardir. Ular koʻp holda yuqori energiya konfiguratsiyasi hisoblanadi. Baʼzi kristallardagi kichik atomlar (asosan kirishmalar) palladiydagi vodorod kabi yuqori energiyasiz oraliqlarni egallashi mumkin.

- Yaqin-atrofdagi vakansiya va interstitsial juftlik Frenkel nuqsoni yoki Frenkel juftligi deb ataladi. Bu ion oraliq joyga oʻtib, boʻsh joy hosil qilganda yuzaga keladi.
- Materiallarni tozalash usullarining asosiy kamchiliklari tufayli materiallar hech qachon 100 % toza boʻlmaydi, bu esa taʼrifi boʻyicha kristallografik nuqsonlarni keltirib chiqaradi. Sof boʻlmagan kristallda begona atom boʻsh tugunga joylashadi. Bunday nuqson vakansiya ham emas, tugunlar aro nuqson ham emas u oʻrinbosar nuqson deb ataladi. Aslida ushbu begona atom kristalning biron bir joyida boʻlmasligi kerak edi, ammo bu atomning mavjudligi nosoflikni paydo qiladi. Baʼzi hollarda oʻrinbosar atom (ion) radiusi u oʻrnini bosayotgan atom (ion)nikidan sezilarli darajada kichikroq boʻlsa, uning muvozanat holati panjara joyidan uzoqlashishi mumkin. Ushbu turdagi almashtirish nuqsonlari koʻpincha markazdan tashqari ionlar deb ataladi. Oʻrinbosar nuqsonlarning ikki xil turi mavjud: Izovalent almashtirish va aliovalent almashtirish. Izovalent almashtirishda tugunga asl ionning oʻrniga shu ion bilan bir xil oksidlanish darajasiga ega boʻlgan boshqa ion kiritiladi. Aliovalent almashtirishda esa asl ionni oʻrniga shu iondan farqli oksidlanish darajasiga ega boʻlgan ion kiritiladi. Aliovalentli almashtirishlarda ion birikmasi ichidagi umumiy zaryad miqdori oʻzgaradi, biroq ionli birikmaning zaryadi neytral holda qolishi kerak. Shuning uchun neytrallikni taʼminlash mexanizi talab qilinadi. Demak, metallardan biri qisman yoki toʻliq oksidlanadi yoki qaytariladi, yoki ion boʻshliqlari hosil boʻladi.
- Antizit nuqsonlari[5][6] tartiblangan qotishma yoki birikmada har xil turdagi atomlar oʻrin almashganda yuzaga keladi. Masalan, baʼzi qotishmalar muntazam tuzilishga ega boʻlib, unda har bir boshqa atom har xil turdagi; Misol uchun, A tipidagi atomlar kubik panjaraning burchaklarida, B tipidagi atomlar esa kublarning markazida joylashgan deb faraz qilaylik. Agar bitta kubning markazida A atomi boʻlsa, atom odatda B atomi egallagan joyda joylashgan va shuning uchun antizit nuqsoni hisoblanadi. Bu na boʻsh joy, na interstitsial, na nopoklik.
- Topologik nuqsonlar kristalning oddiy kimyoviy bogʻlanish muhiti topologik jihatdan atrofdagilardan farq qiladigan hududlardir. Masalan, grafitning mukammal varagʻida (grafen) barcha atomlar oltita atomdan iborat halqalarda joylashgan. Agar varaqda halqadagi atomlar soni oltidan farq qiladigan mintaqalar boʻlsa, atomlarning umumiy soni bir xil boʻlib qolsa, topologik nuqson paydo boʻldi. Bunga misol qilib nanotubalardagi Tosh Uels nuqsoni boʻlib, u ikkita qoʻshni 5 aʼzoli va ikkita 7 aʼzoli atom halqalaridan iborat.

- Shuningdek, amorf qattiq moddalarda ham nuqsonlar boʻlishi mumkin. Tabiiyki, ularni aniqlash biroz qiyinchilik tugʻdiradi, lekin baʼzida ularning tabiatini oson tushunish mumkin. Masalan, ideal bogʻlangan amorf kremniy dioksidda barcha Si atomlari O atomlari bilan 4 ta, barcha O atomlari esa Si atomi bilan 2 ta bogʻga ega. Shunday qilib, masalan, faqat bitta Si bogʻiga ega boʻlgan O atomini (sarsayotgan bogʻlanish) kremniyning nuqsoni deb hisoblash mumkin[7]. Bundan tashqari, nuqsonlar boʻsh yoki zich joylashgan lokal atom qoʻshnilariga asoslangan amorf qattiq jismlarda ham aniqlanishi mumkin va bunday „nuqsonlar“ ning xossalari kristallardagi oddiy vakansiyalar va interstitsiallarga oʻxshashligini koʻrsatish mumkin
- Turli xil nuqtaviy nuqsonlar orasida komplekslar paydo boʻlishi mumkin. Misol uchun, agar boʻsh joy nosoflikka duch kelsa va nosoflik panjara uchun juda katta boʻlsa, ikkalasi bir-biriga bogʻlanishi mumkin. Interstitsiallar „boʻlingan interstitsial“ yoki „gantel“ tuzilmalarini hosil qilishi mumkin, bu yerda ikkita atom atom maydonini samarali ravishda baham koʻradi, natijada hech bir atom bu joyni egallamaydi[8][9].
Chiziqli nuqsonlar
[tahrir | manbasini tahrirlash]Chiziqli nuqsonlar oʻlchov nazariyalari bilan tavsiflanishi mumkin.
Dislokatsiyalar chiziqli nuqsonlar boʻlib, ular atrofida kristall panjaraning atomlari notoʻgʻri joylashadi[10]. Dislokatsiyaning ikkita asosiy turi mavjud: chekka dislokatsiya va vintli dislokatsiya. Ikkala turning xossalarini oʻzida namoyish qilgan nuqsonlar, yaʼni „aralash“ dislokatsiyalar ham keng tarqalgan.
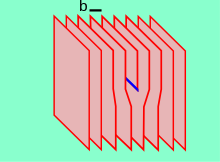
Chekka dislokatsiyasi kristallning oʻrtasida joylashgan atomlar tekisligining tugashi natijasida yuzaga keladi. Bunday holatda, qoʻshni tekisliklar toʻgʻri emas, balki uning oʻrniga tugallanmagan tekislik chetiga egiladi va kristall struktura har ikki tomondan mukammal tarzda tartibga solinadi. Misol sifatida qogʻozlar toʻplamini olish mukin: agar qogʻoz toʻplamiga yarim qogʻoz qoʻyilgan boʻlsa, dastadagi nuqson faqat yarim varaqning chetida seziladi.
Vintsimon dislokatsiyasini tasavvur qilish qiyinroq, lekin bunday nuqsonlarda asosan kristall panjaradagi atomlarning atom tekisliklari chiziqli nuqson (dislokatsiya chizigʻi) atrofida spiral yoʻl hosil qilgan strukturani oʻz ichiga oladi.
Dislokatsiyaning mavjudligi panjarada mexanik kuchlanish (burilish) hosil boʻlishiga olib keladi. Bunday buzilishning yoʻnalishi va kattaligi Burgers vektori (b) bilan ifodalanadi. Chekka turdagi nuqson uchun b dislokatsiya chizigʻiga perpendikulyar, vintsimon nuqsonda esa parallel boʻladi. Metall materiallarda b yaqin oʻralgan kristallografik yoʻnalishlarga toʻgʻri keladi va uning kattaligi bitta atomlararo masofaga teng.
Dislokatsiyalar, agar qoʻshni tekislik atomlari bilan bogʻlanish uzilsa va oxirgi chekkadagi atomlar bilan qayta bogʻlansa, harakatlanishi mumkin.
Bunday dislokatsiyalarning mavjudligi va ularning tashqi yuklar hosil qilgan stresslar taʼsirida osongina harakat qilish (va oʻzaro taʼsir qilish) qobiliyati metall materiallarning xarakterli egiluvchanligiga olib keladi.
Dislokatsiyalarni transmissiya elektron mikroskopiya, maydon ion mikroskopiyasi va atom zond texnikasi yordamida kuzatish mumkin. Chuqur darajadagi qisqa vaqtli spektroskopiya yarimoʻtkazgichlarda, asosan, kremniydagi dislokatsiyalarning elektr faolligini oʻrganish uchun ishlatiladi.
Dislokatsiyalar — bu chiziq atrofidagi burchakni „qoʻshish“ yoki „ayirish“ ga mos keladigan chiziq nuqsonlar. Asosan, bu shuni anglatadiki, agar siz chiziq nuqsoni atrofida kristall yoʻnalishini kuzatsangiz, aylanish hosil boʻlishini koʻrasiz. Odatda, ular faqat suyuq kristallarda rol oʻynaydi deb oʻylangan edi, ammo soʻnggi kuzatishlar ular qattiq materiallarda ham rol oʻynashi mumkinligini koʻrsatmoqda, masalan, yoriqlarning oʻz-oʻzini tiklashiga olib keladi[11].
Tekislik nuqsonlari
[tahrir | manbasini tahrirlash]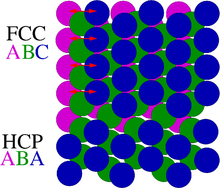
- Don chegaralari strukturaningning kristallografik yoʻnalishi keskin oʻzgargan joyda paydo boʻladi. Bu odatda ikkita kristal alohida oʻsishni boshlab, keyin qayta uchrashganda sodir boʻladi.
- Antifaza chegaralari tartiblangan qotishmalarda paydo boʻladi: bu holda, kristallografik yoʻnalish bir xil boʻlib qoladi, lekin chegaraning har bir tomoni qarama-qarshi fazaga ega: Masalan, tartib odatda ABABABAB (olti burchakli yaqin oʻralgan kristal) boʻlsa, antifaza chegarasi ABABBABA shaklni oladi.
- Stacking nosozliklari bir qator kristall tuzilmalarda sodir boʻladi, ammo umumiy misol yaqin oʻralgan tuzilmalarda. Ular kristalldagi qatlamlarning stacking ketma-ketligining mahalliy ogʻishi natijasida hosil boʻladi. Bunga ABABCABAB stacking ketma-ketligi misol boʻla oladi.
- Egizak chegara — kristallning tartibida oyna simmetriya tekisligini kirituvchi nuqson. Misol uchun, kubikli zich oʻralgan kristallarda egizak chegaraning stacking ketma-ketligi ABCABCBACBA boʻladi.
- Yagona kristall tekisliklarida atomik tekis teraslar orasidagi qadamlar ham tekislik nuqsonlari sifatida qaralishi mumkin. Bunday nuqsonlar va ularning geometriyasi organik molekulalarning adsorbsiyasiga sezilarli taʼsir koʻrsatishi koʻrsatilgan[12].
Ommaviy nuqsonlar
[tahrir | manbasini tahrirlash]- Teshiklar, yoriqlar yoki qoʻshimchalar kabi uch oʻlchovli makroskopik yoki ommaviy nuqsonlar
- Boʻshliqlar — atomlar boʻlmagan va boʻsh ish oʻrinlari klasterlari sifatida koʻrib chiqilishi mumkin boʻlgan kichik hududlar.
- Nopokliklar birgalikda toʻplanib, boshqa fazaning kichik hududlarini hosil qilishi mumkin. Ular koʻpincha choʻkma deb ataladi.
Matematik tasniflash usullari
[tahrir | manbasini tahrirlash]Kristallardagi dislokatsiyalar va boshqa nuqsonlar nazariyasi bilan emas, balki suyuq kristallardagi disklinatsiyalar va 3He super suyuqlikdagi qoʻzgʻalishlar uchun ham ishlaydigan jismoniy panjara nuqsonlarini muvaffaqiyatli matematik tasniflash usuli topologik gomotopiya nazariyasidir[13].
Kompyuter simulyatsiyasi usullari
[tahrir | manbasini tahrirlash]Zichlik funksional nazariyasi, klassik molekulyar dinamika va kinetik Monte-Karlo[14] simulyatsiyalari kompyuter simulyatsiyalari yordamida qattiq jismlardagi nuqsonlarning xususiyatlarini oʻrganish va ularni modellashtirish uchun keng qoʻllanadi[15][16][17][18][19][20][21]. Lubachevskiy-Stillinger algoritmidan foydalangan holda har xil oʻlchamdagi qattiq sharlarni va/yoki oʻlchami oʻlchanmaydigan konteynerlarda tiqilib qolishni taqlid qilish kristallografik nuqsonlarning ayrim turlarini koʻrsatishning samarali usuli boʻlishi mumkin[22].
Yana qarang
[tahrir | manbasini tahrirlash]- Bjerrum nuqsoni
- Olmosdagi kristallografik nuqsonlar
- Kröger-Vink belgisi
- F-markazi
Manbalar
[tahrir | manbasini tahrirlash]- ↑ Hong, J.; Hu, Z.; Probert, M.; Li, K.; Lv, D.; Yang, X.; Gu, L.; Mao, N.; Feng, Q. (2015). „Exploring atomic defects in molybdenum disulphide monolayers“. Nature Communications. 6-jild. 6293-bet. Bibcode:2015NatCo...6.6293H. doi:10.1038/ncomms7293. PMC 4346634. PMID 25695374.
- ↑ Siegel, R. W. (1982) Atomic Defects and Diffusion in Metals, in Point Defects and Defect Interactions in Metals, J.-I. Takamura (ED.), p. 783, North Holland, Amsterdam
- ↑ Point Defects in Solids Crawford, J. H.: . New York: Plenum Press, 1975.
- ↑ Watkins, G. D. (1997) „Native defects and their interactions with impurities in silicon“, p. 139 in Defects and Diffusion in Silicon Processing, T. Diaz de la Rubia, S. Coffa, P. A. Stolk, and C. S. Rafferty (eds), vol. 469 of MRS Symposium Proceedings, Materials Research Society, Pittsburgh, ISBN 1-55899-373-8
- ↑ Mattila, T; Nieminen, RM (1995). „Direct Antisite Formation in Electron Irradiation of GaAs“. Physical Review Letters. 74-jild, № 14. 2721–2724-bet. Bibcode:1995PhRvL..74.2721M. doi:10.1103/PhysRevLett.74.2721. PMID 10058001.
- ↑ Hausmann, H.; Pillukat, A.; Ehrhart, P. (1996). „Point defects and their reactions in electron-irradiated GaAs investigated by optical absorption spectroscopy“. Physical Review B. 54-jild, № 12. 8527–8539-bet. Bibcode:1996PhRvB..54.8527H. doi:10.1103/PhysRevB.54.8527. PMID 9984528.
- ↑ Lieb, Klaus-Peter; Keinonen, Juhani (2006). „Luminescence of ion-irradiated α-quartz“. Contemporary Physics. 47-jild, № 5. 305–331-bet. Bibcode:2006ConPh..47..305L. doi:10.1080/00107510601088156.
- ↑ Hannes Raebiger (2010). „Theory of defect complexes in insulators“. Physical Review B. 82-jild, № 7. 073104-bet. Bibcode:2010PhRvB..82g3104R. doi:10.1103/PhysRevB.82.073104.
- ↑
Hannes Raebiger, Hikaru Nakayama, and Takeshi Fujita (2014). „Control of defect binding and magnetic interaction energies in dilute magnetic semiconductors by charge state manipulation“. Journal of Applied Physics. 115-jild, № 1. 012008-bet. Bibcode:2014JAP...115a2008R. doi:10.1063/1.4838016.
{{cite magazine}}: CS1 maint: multiple names: authors list () - ↑ Hirth, J. P.. Theory of dislocations, 2, Krieger Pub Co, 1992. ISBN 978-0-89464-617-1.
- ↑ „Chandler, David L., Cracked metal, heal thyself, MIT news, 9-oktabr 2013-yil“.
- ↑ Waldmann, T. (2012). „The role of surface defects in large organic molecule adsorption: substrate configuration effects“. Physical Chemistry Chemical Physics. 14-jild, № 30. 10726–31-bet. Bibcode:2012PCCP...1410726W. doi:10.1039/C2CP40800G. PMID 22751288.
- ↑ Mermin, N. (1979). „The topological theory of defects in ordered media“. Reviews of Modern Physics. 51-jild, № 3. 591–648-bet. Bibcode:1979RvMP...51..591M. doi:10.1103/RevModPhys.51.591.
- ↑ Cai, W.; Bulatov, V. V.; Justo, J. F.; Argon, A.S; Yip, S. (2000). „Intrinsic mobility of a dissociated dislocation in silicon“. Phys. Rev. Lett. 84-jild, № 15. 3346–3349-bet. Bibcode:2000PhRvL..84.3346C. doi:10.1103/PhysRevLett.84.3346. PMID 11019086.
- ↑ Ashkenazy, Yinon; Averback, Robert S. (2012). „Irradiation Induced Grain Boundary Flow—A New Creep Mechanism at the Nanoscale“. Nano Letters. 12-jild, № 8. 4084–9-bet. Bibcode:2012NanoL..12.4084A. doi:10.1021/nl301554k. PMID 22775230.
- ↑ Mayr, S.; Ashkenazy, Y.; Albe, K.; Averback, R. (2003). „Mechanisms of radiation-induced viscous flow: Role of point defects“. Phys. Rev. Lett. 90-jild, № 5. 055505-bet. Bibcode:2003PhRvL..90e5505M. doi:10.1103/PhysRevLett.90.055505. PMID 12633371.
- ↑ Nordlund, K; Ashkenazy, Y; Averback, R. S; Granato, A. V (2005). „Strings and interstitials in liquids, glasses and crystals“. Europhys. Lett. 71-jild, № 4. 625–631-bet. Bibcode:2005EL.....71..625N. doi:10.1209/epl/i2005-10132-1.
- ↑ Korhonen, T; Puska, M.; Nieminen, R. (1995). „Vacancy formation energies for fcc and bcc transition metals“. Phys. Rev. B. 51-jild, № 15. 9526–9532-bet. Bibcode:1995PhRvB..51.9526K. doi:10.1103/PhysRevB.51.9526. PMID 9977614.
- ↑ Puska, M. J.; Pöykkö, S.; Pesola, M.; Nieminen, R. (1998). „Convergence of supercell calculations for point defects in semiconductors: vacancy in silicon“. Phys. Rev. B. 58-jild, № 3. 1318–1325-bet. Bibcode:1998PhRvB..58.1318P. doi:10.1103/PhysRevB.58.1318.
- ↑ Nordlund, K.; Averback, R. (1998). „The role of self-interstitial atoms on the high temperature properties of metals“. Phys. Rev. Lett. 80-jild, № 19. 4201–4204-bet. Bibcode:1998PhRvL..80.4201N. doi:10.1103/PhysRevLett.80.4201.
- ↑ Sadigh, B; Lenosky, Thomas; Theiss, Silva; Caturla, Maria-Jose; Diaz De La Rubia, Tomas; Foad, Majeed (1999). „Mechanism of Boron Diffusion in Silicon: An Ab Initio and Kinetic Monte Carlo Study“. Phys. Rev. Lett. 83-jild, № 21. 4341–4344-bet. Bibcode:1999PhRvL..83.4341S. doi:10.1103/PhysRevLett.83.4341.
- ↑ Stillinger, Frank H.; Lubachevsky, Boris D. (1995). „Patterns of broken symmetry in the impurity-perturbed rigid-disk crystal“. Journal of Statistical Physics. 78-jild, № 3–4. 1011–1026-bet. Bibcode:1995JSP....78.1011S. doi:10.1007/BF02183698.
Adabiyotlar
[tahrir | manbasini tahrirlash]- Hagen Kleinert, Kondensatsiyalangan materiyadagi oʻlchov maydonlari, Vol. II, „Stress va nuqsonlar“, s. 743-1456, Jahon ilmiy (Singapur, 1989); Qogʻoz muqovaliISBN 9971-5-0210-0
- Hermann Shmalzried: qattiq holat reaktsiyalari. Verlag Chemie, Vaynxaym 1981-yil,ISBN 3-527-25872-8.
